How Do You Find The Volume Of A Gas Given Temperature

The behavior of gases can be described by several laws based on experimental observations of their properties. The pressure of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does not change (Amontons's law). The volume of a given gas sample is directly proportional to its absolute temperature at constant pressure (Charles's law).

The volume of a given amount of gas is inversely proportional to its pressure when temperature is held constant (Boyle's law). Under the same conditions of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro's law). Eventually, these individual laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures.

We will consider the key developments in individual relationships , then put them together in the ideal gas law. There are also terms such as RTP – room temperature and pressure, and SLC – standard laboratory conditions, However, there is no single definition for them, and different organizations can use different definitions. Using this calculator, you can calculate the molar volume of a gas for arbitrary temperature and pressure. Just note that for big values real gases divert from ideal gas law (that's why they are not "ideal") and this formula can't be used.

Avogadro's Number, the ideal gas constant, and both Boyle's and Charles' laws combine to describe a theoretical ideal gas in which all particle collisions are absolutely equal. The laws come very close to describing the behavior of most gases, but there are very tiny mathematical deviations due to differences in actual particle size and tiny intermolecular forces in real gases. Nevertheless, these important laws are often combined into one equation known as the ideal gas law. Using this law, you can find the value of any of the other variables — pressure, volume, number or temperature — if you know the value of the other three.

First, we must determine the question, which is to calculate the volume of a quantity of gas at a given temperature and pressure. In a second step, after establishing a basis, we must convert the mass of methane that will be the basis into pound moles. Third, we must convert temperature in degrees Fahrenheit into absolute degrees Rankin and, fourth, convert pressure from psig into psia.

Fifth, we must select the appropriate ideal gas constant and use it with a rewritten form of Equation 4.11 to determine the volume of 11.0 lbs of methane gas. Finally, we can substitute the values previously determined into the rewritten equation to calculate the volume. The attraction or repulsion between the individual gas molecules and the container are negligible. Further, for an ideal gas, the molecules are considered to be perfectly elastic and there is no internal energy loss resulting from collision between the molecules. Such ideal gases are said to obey several classical equations such as the Boyle's law, Charles's law and the ideal gas equation or the perfect gas equation. We will first discuss the behavior of ideal gases and then follow it up with the behavior of real gases.

We have just seen that the volume of a specified amount of a gas at constant pressure is proportional to the absolute temperature. In addition, we saw that the volume of a specified amount gas at a constant temperature is also inversely proportional to its pressure. We can correctly assume that pressure of a specified amount of gas at a constant volume is proportional to its absolute temperature.

Let us also add the fact that the volume at constant pressure and temperature is also proportional to the amount of gas. Similarly, the pressure at constant volume and temperature is proportional to the amount of gas. Thus, these laws and relationships can be combined to give Equation 4.10. Gases whose properties of P, V, and T are accurately described by the ideal gas law are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter.

Although all the calculations presented in this module assume ideal behavior, this assumption is only reasonable for gases under conditions of relatively low pressure and high temperature. In the final module of this chapter, a modified gas law will be introduced that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures. Plots of the volume of gases versus temperature extrapolate to zero volume at −273.15°C, which is absolute zero , the lowest temperature possible.

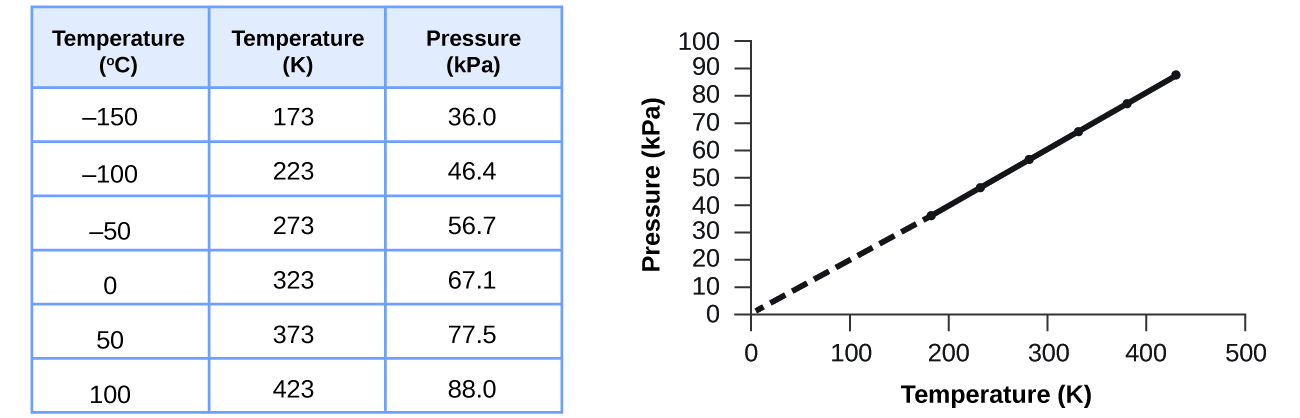
Charles's law implies that the volume of a gas is directly proportional to its absolute temperature. This relationship between temperature and pressure is observed for any sample of gas confined to a constant volume. An example of experimental pressure-temperature data is shown for a sample of air under these conditions in . An example of experimental pressure-temperature data is shown for a sample of air under these conditions in Figure 9.11.

The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure of 1 atm. If the temperature is in kelvin, volume and temperature are directly proportional. Charles's law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant. But something happens to the validity of this assumption as the gas is compressed.

Imagine for the moment that the atoms or molecules in a gas were all clustered in one corner of a cylinder, as shown in the figure below. At normal pressures, the volume occupied by these particles is a negligibly small fraction of the total volume of the gas. As a result, real gases are not as compressible at high pressures as an ideal gas.

The volume of a real gas is therefore larger than expected from the ideal gas equation at high pressures. Constant into the ideal gas equation that was equal to the volume actually occupied by a mole of gas particles. Because the volume of the gas particles depends on the number of moles of gas in the container, the term that is subtracted from the real volume of the gas is equal to the number of moles of gas times b.

Thus the ideal gas law does a good job of approximating the behavior of real gases at STP. As the pressure on a gas increases, the volume of the gas decreases because the gas particles are forced closer together. Conversely, as the pressure on a gas decreases, the gas volume increases because the gas particles can now move farther apart.

When a gas behaves like an ideal gas, we can calculate its volume by measuring its temperature, pressure, and moles and plugging them into the ideal gas equation. When the concentration of a gas is very high, however, the real or measured volume is greater than the volume that would be calculated from the ideal gas equation. The reason is that small as the particles of a gas are, they do constitute part of its volume. In other words, the real volume of a gas is equal to the volume that the particles themselves occupy plus the volume of the empty space between the particles. Previously, we considered only ideal gases, those that fit the assumptions of the ideal gas law. When pressure is low and temperature is low, gases behave similarly to gases in the ideal state.

When pressure and temperature increase, gases deviate farther from the ideal state. We have to assume new standards, and consider new variables to account for these changes. A common equation used to better represent a gas that is not near ideal conditions is the van der Waals equation, seen below. You can adapt to the set of units you'd like to use just by changing the gas constant. Here are the constants and the units of pressure, temperature and volume that go with them. While, when using gas laws like Charles' law and the Gay-Lussac law, it's OK to use Celsius temperatures , it's important to use Kelvin temperatures in the ideal gas law.

While ideal gases are strictly a theoretical conception, real gases can behave ideally under certain conditions. Similarly, high-temperature systems allow for the gas particles to move quickly within the system and exhibit less intermolecular forces with each other. Therefore, for calculation purposes, real gases can be considered "ideal" in either low pressure or high-temperature systems.

Is defined as a hypothetical gaseous substance whose behavior is independent of attractive and repulsive forces and can be completely described by the ideal gas law. In reality, there is no such thing as an ideal gas, but an ideal gas is a useful conceptual model that allows us to understand how gases respond to changing conditions. As we shall see, under many conditions, most real gases exhibit behavior that closely approximates that of an ideal gas. The ideal gas law can therefore be used to predict the behavior of real gases under most conditions.

As you will learn in Section 10.8 "The Behavior of Real Gases", the ideal gas law does not work well at very low temperatures or very high pressures, where deviations from ideal behavior are most commonly observed. The ideal gas law formula states that pressure multiplied by volume is equal to moles times the universal gas constant times temperature. If we partially fill an airtight syringe with air, the syringe contains a specific amount of air at constant temperature, say 25 °C. This example of the effect of volume on the pressure of a given amount of a confined gas is true in general.

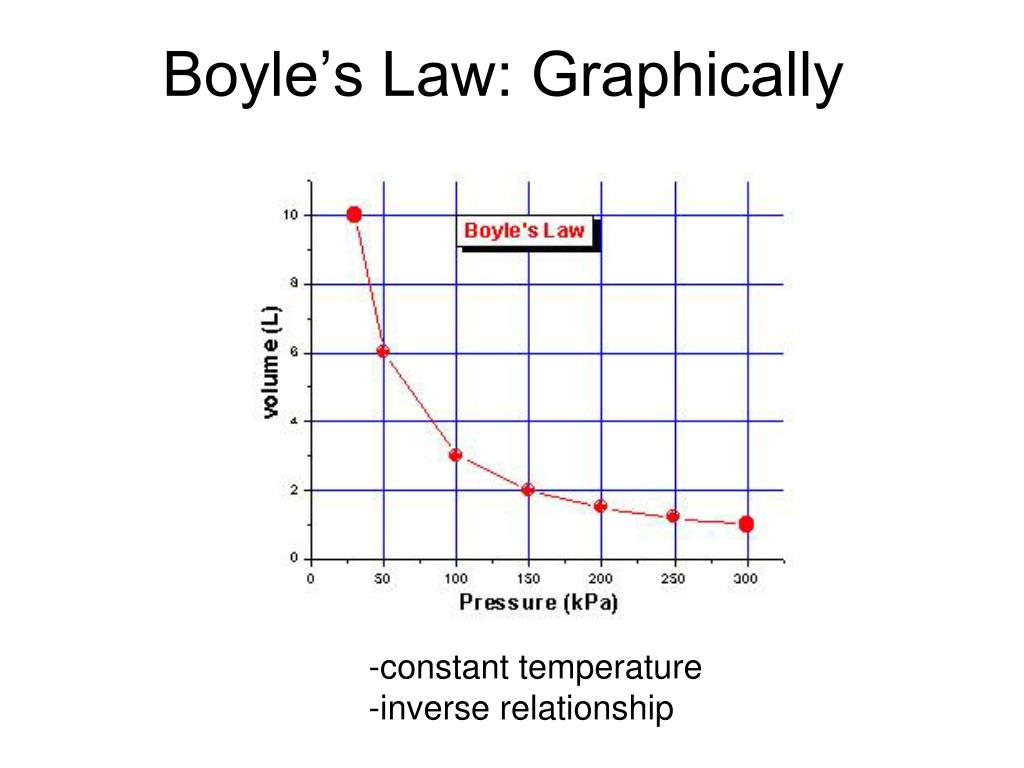
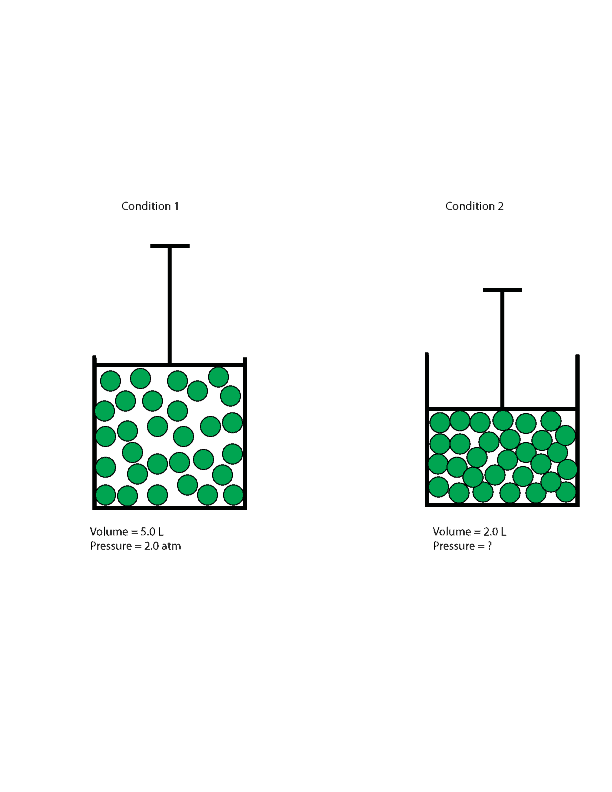
Decreasing the volume of a contained gas will increase its pressure, and increasing its volume will decrease its pressure. In fact, if the volume increases by a certain factor, the pressure decreases by the same factor, and vice versa. Volume-pressure data for an air sample at room temperature are graphed in . Volume-pressure data for an air sample at room temperature are graphed in Figure 9.13. Volume-pressure data for an air sample at room temperature are graphed in Figure 5. The behavior of real gases usually agrees with the predictions of the ideal gas equation to within 5% at normal temperatures and pressures.

At low temperatures or high pressures, real gases deviate significantly from ideal gas behavior. Any gas particle possesses a volume within the system , which violates the first assumption. Additionally, gas particles can be of different sizes; for example, hydrogen gas is significantly smaller than xenon gas. Gases in a system do have intermolecular forces with neighboring gas particles, especially at low temperatures where the particles are not moving quickly and interact with each other. Even though gas particles can move randomly, they do not have perfect elastic collisions due to the conservation of energy and momentum within the system.

A common use of Equation 10.23 is to determine the molar mass of an unknown gas by measuring its density at a known temperature and pressure. This method is particularly useful in identifying a gas that has been produced in a reaction, and it is not difficult to carry out. A flask or glass bulb of known volume is carefully dried, evacuated, sealed, and weighed empty. It is then filled with a sample of a gas at a known temperature and pressure and reweighed.

The difference in mass between the two readings is the mass of the gas. The volume of the flask is usually determined by weighing the flask when empty and when filled with a liquid of known density such as water. The use of density measurements to calculate molar masses is illustrated in Example 10.

It is important to check your answer to be sure that it makes sense, just in case you have accidentally inverted a quantity or multiplied rather than divided. Because we know that gas volume decreases with decreasing temperature, the final volume must be less than the initial volume, so the answer makes sense. We could have calculated the new volume by plugging all the given numbers into the ideal gas law, but it is generally much easier and faster to focus on only the quantities that change.

The ideal gas law allows us to calculate the value of the fourth variable for a gaseous sample if we know the values of any three of the four variables . It also allows us to predict the final state of a sample of a gas (i.e., its final temperature, pressure, volume, and amount) following any changes in conditions if the parameters are specified for an initial state. Some applications are illustrated in the following examples.

The approach used throughout is always to start with the same equation—the ideal gas law—and then determine which quantities are given and which need to be calculated. Let's begin with simple cases in which we are given three of the four parameters needed for a complete physical description of a gaseous sample. Of the three states of matter, gases undergo the greatest volume changes with changing temperature and pressure conditions, but liquids also undergo changes. Liquids aren't responsive to pressure changes, but they can be responsive to temperature changes, depending on their composition. To calculate the volume change of a liquid with respect to temperature, you need to know its coefficient of volumetric expansion. Gases, on the other hand, all expand and contract more or less in accordance with the ideal gas law, and the volume change is not dependent on its composition.

Kinetic particle reasoning - increasing the temperature increases the kinetic energy of the molecules giving more forceful collisions which push out the gas at constant pressure. In another lesson, you learned about ideal gases and the ideal gas equation. But since real gases behave similarly to ideal gases at normal temperatures and pressures, we can use the ideal gas equation to predict the behavior of real gases under these conditions. Picture yourself riding on an H2O molecule in water vapor heated to a relatively high temperature. As long as the temperature remains high, however, the rapidly moving water molecules break the attraction almost immediately and continue on their separate paths. Because, the particles in a gas at high temperature spend only a small fraction of their time experiencing these short-lived attractions, the effect of the attractions on the properties of the gas is negligible.

We can therefore consider a gas at high temperature to be an ideal gas, with no attractions between the particles. The van der Waals equation contains two constants, a and b, that are characteristic properties of a particular gas. The first of these constants corrects for the force of attraction between gas particles. Compounds for which the force of attraction between particles is strong have large values for a. If you think about what happens when a liquid boils, you might expect that compounds with large values of awould have higher boiling points. Gases with very small values of a, such as H2 and He, must be cooled to almost absolute zero before they condense to form a liquid.

A law that states that at constant temperature and pressure, the volume of a sample of gas is directly proportional to the number of moles of gas in the sample. At constant pressure, the volume of a gas is proportional to the absolute temperature. (Law of Gay-Lussac) The pressures on the inside and outside of the inflated balloon are nearly equal. The pressure on the outside is the constant atmospheric pressure. The pressure in the freezer is atmospheric pressure, the temperature in the freezer is lower that the outside temperature, so the volume of the balloon decreases when it is placed into the freezer. This relationship shows us that the only way to increase the volume of gas, V, while maintaining the same temperature and pressure, is to increase the moles of gas, n, that are present, that is, add more gas.

This relationship shows us that if we increase the moles of gas, n, by adding more gas while maintaining the same temperature and pressure, the volume of gas, V, will also increase. Decreasing the volume of the container forces the particles to collide more often, so the pressure is increased. A good example of this is when you fill a tire with air. As more air goes in, the gas molecules get packed together, reducing their volume. As long as the temperature stays the same, the pressure increases.